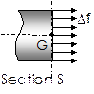Résistance des matériaux

La résistance des matériaux a trois objectifs principaux :

•  la connaissance des caractéristiques mécaniques des matériaux. (comportement sous l’effet d’une action mécanique)

•  l'étude de la résistance des pièces mécaniques. (résistance ou rupture)

•  l'étude de la déformation des pièces mécaniques.

Ces études permettent de choisir le matériau et les dimensions d'une pièce mécanique en fonction des conditions de déformation et de résistance requises.

1 Hypothèse de la théorie sur la résistance des matériaux

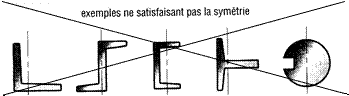
· Notion de poutre : On appellera poutre toute pièce mécanique sur laquelle des calculs de RDM pourront être effectués et qui  répond aux critères suivants :

- Une poutre est un solide long par rapport aux dimensions des sections droites. (L>10D pour avoir un résultat précis…)

- La Ligne moyenne ou fibre neutre est le lieu des centres de gravité de toutes les sections droites du solide

(A, G, B,….)

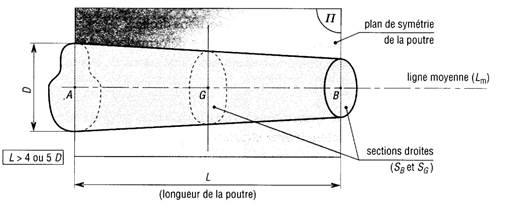
-     La poutre doit comporter un plan de symétrie longitudinal noté (p).

- Les sections droites (S) doivent rester constantes ou ne varier que progressivement entre A et B (pas de variation brusque de section).

Remarque : La fibre neutre est la seule à ne pas subir de variation de longueur après déformation.

Exemples de poutres

· Hypothèses sur les matériaux

L’homogénéité : on admet que les matériaux ont les mêmes propriétés mécaniques en tous points ( matériaux parfaits sans défauts).

L’Isotropie : on admet que les matériaux ont, en un même point, le même comportement dans toutes les directions (valable uniquement pour les matériaux non fibrés : hypothèse non valable pour le bois par exemple…).

· Hypothèses sur les forces extérieures

Plan de symétrie : Toutes les forces extérieures sont contenues dans le plan de symétrie de la poutre, ou alors disposées symétriquement par rapport à ce plan.

Types d’actions mécaniques extérieures : Deux types d’actions mécaniques peuvent s’exercer sur la poutre :                   - Charges concentrées : forces ou moments

    - Charges réparties.

· Hypothèses sur les déformations

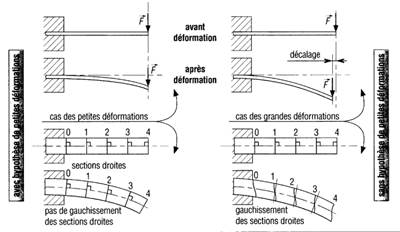
Hypothèse de Navier et  Bernouilli : Les sections planes et perpendiculaires à la ligne moyenne (section droite) avant déformation, restent planes et perpendiculaires à la ligne moyenne après déformation.

Amplitude des déformations : On se place toujours dans le cas de petites déformations (les déformations restent faibles par rapport aux dimensions de la poutre). On peut donc admettre que les forces extérieures conservent une direction fixe avant et après déformation.

2 Sollicitation

2-1 Sollicitation simple : Ce sont des actions mécaniques appliquées à un solide (2 actions égales et opposées).

2-2 Autres sollicitations :

· Fatigue : Les pièces soumises à de fortes vibrations peuvent se rompre au bout d’un certain temps de service si les amplitudes de contrainte sont trop élevées  Les pièces soumises à de fortes vibrations peuvent se rompre au bout d’un certain temps de service si les amplitudes de contrainte sont trop élevées.

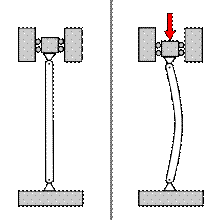
· Flambage : certains éléments, comme les colonnes droites élancées chargées en compression, peuvent subir un changement de forme brutal (courbure) pour une valeur critique de la charge

· Matage : Écrasement localisé de la matière dû à un champ de pression trop élevé dans une zone de contact entre deux pièces. Le matage correspond en général à une déformation plastique.

· Le fluage : est un phénomène physique qui provoque la déformation irréversible d’un matériau soumis à une contrainte constante pendant une durée donnée.

· Relaxation : une déformation est imposée brusquement, puis elle est maintenue constante. La contrainte qui en résulte diminue progressivement au cours du temps  alors que la déformation viscoplastique continue d’augmenter.

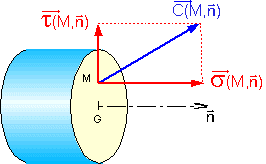
3 Contrainte :

Les contraintes représentent les efforts de cohésion dans un solide qui permettent à la matière à résister aux sollicitations. Les contraintes sont issues d'interaction entre des petites parties de la matière (cristaux, molécules ...). L'équivalent de la contrainte pour un fluide parfait est la pression. Unité le Pa (Pascal)

On note: C(M,n) la contrainte en M pour la coupure orientée par n. La contrainte est projetée: σ sur n pour donner la contrainte normale (sigma) τ dans le plan de coupure pour donner la contrainte tangentielle (tau) (nommée aussi contrainte de cission ou de cisaillement)

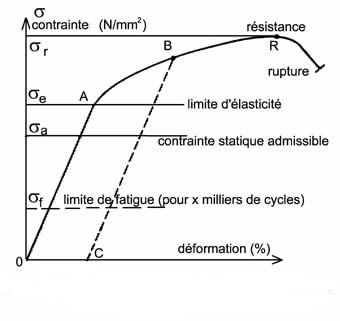
Contrainte maximum, contrainte limite et contrainte admissible

Facteur de charge : C'est une grandeur qui traduit l'effort appliqué à la structure de l'aéronef. Le facteur de charge est le rapport entre la charge totale supportée par la structure d’un appareil et le poids réel de cet appareil.

4 Déformation

4-1 Caractérisation qualitative des déformations

4-1-1 Allongement : DL

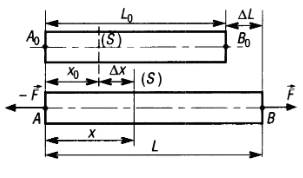
Soit e l’allongement relatif

e = DL / L₀

L’allongement est proportionnel à la longueur initiale de la poutre pour un même effort.

4-1-2 Contraction latérale - Coefficient de poisson

Le coefficient de poisson n (Nu) est le rapport entre la contraction latérale e_d et l’allongement relatif e_L

n=- e_d/e_L

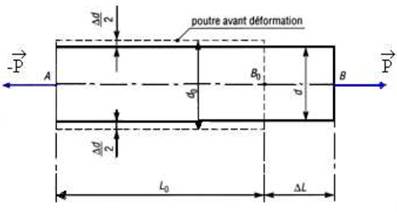
e_L = DL / L₀

e_d = Dd / D₀

4-1-3 Module d’élasticité

Dans un grand nombre de matériaux, il existe une zone élastique pour laquelle l’effort est proportionnel à la déformation.

contrainte = module d’élasticité x déformation

En traction : σ= E x eL

E : Module d’élastisité (de Young) en MPa

4-2 Caractérisation quantitative de l’état de contrainte et des déformations pour la traction et le cisaillement

4-2-1 TRACTION

4-2-1-1 Définitions

Une poutre est sollicitée en traction lorsque les actions aux extrémités se réduisent à deux forces égales et opposées, portées par la ligne moyenne Lm.

L’effort F est appelé effort normal, il est noté N. Quelle que soit la section considérée de la poutre, il s’exerce toujours N au barycentre G de la section.

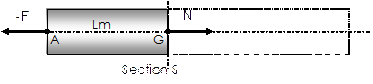
4-2-1-2 Contrainte normale : s

s : contrainte normale en Mpa ou en N/mm² N : effort normal en N S : aire de la section droite en mm²

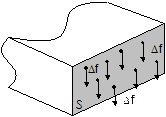
Chaque élément de surface DS supporte un effort de traction Df parallèle à la ligne moyenne. Il y a répartition uniforme des contraintes dans la section droite. D’où : s =

4-2-1-3 Condition de résistance

Alors, la condition de résistance s’écrit :

s_maxi £ R_pe

Avec :       R_e la résistance élastique du matériau (en Mpa) ;

                  s un coefficient de sécurité ;

                  R_pe la résistance pratique à l’extension, avec R_pe = R_e/s ;

4-2-1-4 Déformation

Loi de Hooke :

En déformation élastique, la contrainte s varie linéairement en fonction de l’allongement relatif eL.

s : contrainte normale en N/mm²

E : module d’élasticité longitudinale en Mpa

eL : allongement relatif (pas d’unité)

s = E. eL

Une pièce sollicitée à une traction ou à une compression  subit une déformation appelée DL.

         F x L

DL =                        

                     E x S

4-2-2 CISSAILLEMENT

4-2-2-1 Définitions

Une poutre est sollicitée en cisaillement lorsque sa section S est soumise à une résultante T appliquée en G (barycentre de la section) et contenue dans le plan (S). T est appelé effort tranchant.

4-2-2-2 Contrainte de cisaillement

τ : contrainte tangentielle en Mpa ou N/mm² T : effort tranchant en N S : aire de la section droite cisaillée en mm²

Chaque élément de surface DS supporte un effort de cisaillement Df contenu dans le plan (S). Il y a répartition uniforme des contraintes dans la section droite. D’où : τ =

4-2-2-3 Condition de résistance

Alors, la condition de résistance s’écrit :

τ £ Rpg

Avec :             R_eg la résistance élastique au cisaillement du matériau (en Mpa) ;

                        s un coefficient de sécurité ;

                        R_pg la résistance pratique au cisaillement, avec R_pg = R_eg/s ;

4-2-2-4 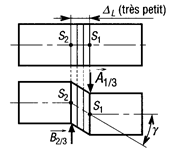Déformation

En déformation élastique, la contrainte de cisaillement τ varie linéairement en fonction de l’angle de glissement g.

τ : contrainte tangentielle en N/mm²

G : module d’élasticité transversal en Mpa

g : angle de glissement en radians

τ = G. g

5 Caractéristique, propriété et identification des matériaux

5-1 Matériaux ferreux et non ferreux (acier utilisés sur aéronefs)

Aciers à usage général et aciers non alliés :

Nuances	R min  Mpa	Re min  Mpa	Nuances	R min  Mpa	Re min  Mpa
S185 (A33)	290	185	C25 (XC25)	460	285
S275 (E28)	410	275	C35 (XC38)	570	335
E295 (A50)	470	295	C45 (XC48)	660	375
E360 (A70)	670	360	C55 (XC54)	730	420
C22 (XC18)	410	255	C60 (XC60)	---	HRC ³ 57

quelques valeurs de E :           

Acier :             E = 200 000 MPa

                                         Fonte :            E = 60 000 à 160 000 MPa

                                         Cuivre :           E = 120 000 MPa

                                         Aluminium :    E = 70 000 MPa

5-2 Traitement thermique

Acier 0,08 %C – 0,4 %Si 16,9 %Cr

Caractéristique mécanique	800°C + refroidissement air	800°C + refroidissement air + revenue de 4h à 450 °C
Résistance (MPa)	572	587
Limite d’élasticité (MPa)	324	392
Allongement à la rupture (%)	22.8	23.6
Résilience (J/cm²)	120	14

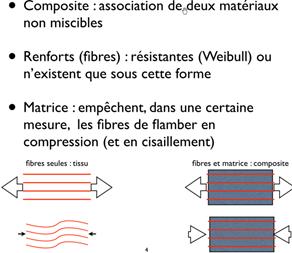
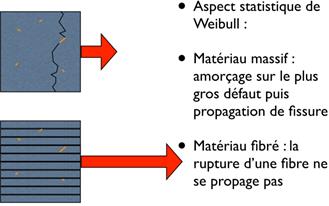
5-3 Matériaux composite et non métallique

5-4 Mastic et résine